this post was submitted on 25 Jun 2025
1 points (100.0% liked)
Science Memes
15551 readers
270 users here now
Welcome to c/science_memes @ Mander.xyz!
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules
- Don't throw mud. Behave like an intellectual and remember the human.
- Keep it rooted (on topic).
- No spam.
- Infographics welcome, get schooled.
This is a science community. We use the Dawkins definition of meme.
Research Committee
Other Mander Communities
Science and Research
Biology and Life Sciences
- !abiogenesis@mander.xyz
- !animal-behavior@mander.xyz
- !anthropology@mander.xyz
- !arachnology@mander.xyz
- !balconygardening@slrpnk.net
- !biodiversity@mander.xyz
- !biology@mander.xyz
- !biophysics@mander.xyz
- !botany@mander.xyz
- !ecology@mander.xyz
- !entomology@mander.xyz
- !fermentation@mander.xyz
- !herpetology@mander.xyz
- !houseplants@mander.xyz
- !medicine@mander.xyz
- !microscopy@mander.xyz
- !mycology@mander.xyz
- !nudibranchs@mander.xyz
- !nutrition@mander.xyz
- !palaeoecology@mander.xyz
- !palaeontology@mander.xyz
- !photosynthesis@mander.xyz
- !plantid@mander.xyz
- !plants@mander.xyz
- !reptiles and amphibians@mander.xyz
Physical Sciences
- !astronomy@mander.xyz
- !chemistry@mander.xyz
- !earthscience@mander.xyz
- !geography@mander.xyz
- !geospatial@mander.xyz
- !nuclear@mander.xyz
- !physics@mander.xyz
- !quantum-computing@mander.xyz
- !spectroscopy@mander.xyz
Humanities and Social Sciences
Practical and Applied Sciences
- !exercise-and sports-science@mander.xyz
- !gardening@mander.xyz
- !self sufficiency@mander.xyz
- !soilscience@slrpnk.net
- !terrariums@mander.xyz
- !timelapse@mander.xyz
Memes
Miscellaneous
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
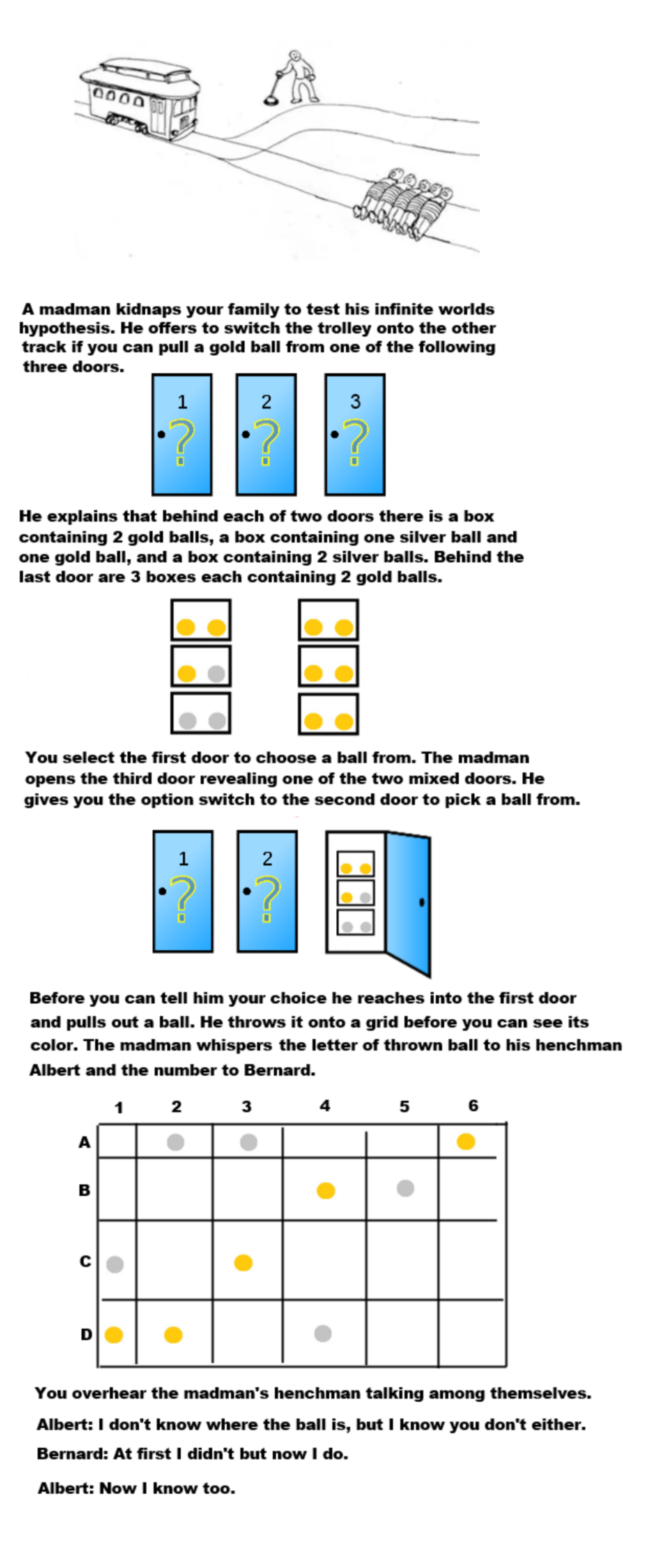
The ball grid problem
Albert knows that Albert doesn't know where the ball is, and also knows that Bernard doesn't know where the ball is, which means the ball is in a row where every ball has another ball in its column, which narrows it to C or D
The information that the ball must be in C or D is enough to exactly select the ball given knowledge of the column, which makes it either C3, D2 or D4
The information that Albert knows which cell it is once Albert knows that Bernard knows means that it must be C3 because if it was a D cell then Albert would still not know
C3 is the ball that was pulled from door 1, thus there was a gold ball behind door 1
Monty hall problem
Which means we dont know whether there were 6 or 3 gold behind door 1, which means its essentially a slightly different Monty Hall problemThe first door either has 2 gold balls (and 3 silver) behind it or 5 gold balls, and the second door either has 3 gold balls and 3 silver or 6 gold balls
The second door has a 66% chance of having 6 gold balls (guaranteed gold) and a 33% chance of having 3/3
The first door has a 66% chance of 2/3 and a 33% chance of 5 (guaranteed gold)
Thus door 1 has a 2/3x2/5 + 1/3 = 3/5 chance of you pulling a gold ball
Door 2 has a 2/3 + 1/3x1/2 = 5/6 chance of pulling a gold ball
You should switch doors to maximise your chance of being allowed to swap tracks
Knowing that the ball was gold gives you Bayesian knowledge about the boxes behind the door, since the prior probability of the host pulling a gold ball from a 6-gold door is different than from the 3/3 door. So you have to multiply Monty Hall probabilities and Bayesian probabilities together.
That assumes the host pulled a ball at random, of course, and not a deliberately gold ball.
Hmm, you're quite right. My intuition is that the Bayesian portion would exactly offset the Monty hall portion. I think, at a glance, Bayes would give door 1 a 2/3 probability of having 6 gold, but Monty Hall would give door 2 the same probability, so we can effectively cancel these out and just consider a raw probability
You either have 5 gold or 2 gold 3 silver behind door 1, and 6 gold or 3 and 3 behind door 2, which gives door 2 a very slight edge. Does that check out?
Yes! Cancels out, leaving only a very slight edge on door 2. All that work for only... 2.77% edge over picking at random. What a troll problem, huh?
Heh what a trolly problem indeed